Rebalancing is one other free lunch in the financial market beyond diversification. This article will discuss rebalancing strategies from four aspects.

It's well-known that high returns often imply high risk, and taking on high risk often implies high returns. However, neither statement is entirely accurate. The first half is true in most cases, but the second half is usually false. High absolute returns generally symbolise high risk, but some alpha strategies can achieve high returns with low risk. These strategies are typically scarce and secretive, so we won’t delve into them here. The second half of the statement often doesn't hold for the general public, who typically experience a high return gap. In other words, their returns are much lower than passive market returns, reflecting that they are often engaged in low-return, high-risk investments. Why is this the case? It's because most of the risks they take are idiosyncratic, without a premium to compensate; furthermore, the public's lack of financial knowledge/gambling mentality leads to behaviours that chase lottery-like negative return assets.

I believe there will be opportunities to discuss the findings mentioned briefly above in more detail in the future. Today, I want to talk about something more pleasant: increasing returns while reducing risk, with the magic of rebalancing.

Whenever something like increasing returns while reducing risk comes up, the efficient market hypothesis is laughed at. Here, I want to say that I believe the market is efficient in most cases. Even if it is inefficient, it doesn’t mean someone can benefit from it; in fact it is incredibly difficult to generate alpha from the market. This is true for professional investors and even more so for retail investors.

For both rebalancing and diversification, the reduced risk is the uncompensated risk, hence the increased return from risk-adjusted perspective. This has nothing to do with the efficient market hypothesis and is more about reducing one’s mistakes to improve long-term wealth.

What is Rebalancing?

What is rebalancing? The definition is straightforward: rebalancing involves adjusting the weights of various assets in your portfolio periodically to align with their initial weights. A simple example is a classic 60/40 stock-bond portfolio. Suppose stocks return 10% in one year, while bonds return 2%. After one year, the stock weight will have increased to 61.8%, and the bond weight will have decreased to 38.2%. The rebalancing process involves selling some stocks and buying some bonds to maintain the 60/40 ratio.

It doesn’t sound special; it might even seem like gambling. Over the past year, stocks have outperformed bonds, and rebalancing would sell the winner and buy the loser, a typical retail investor behavior. How could this create value? Moreover, rebalancing itself introduces transaction costs. If the future is random, the decision to rebalance is value-destroying. Successful strategies can fail due to transaction costs and management fees, let alone rebalancing, which is a negative-sum game.

Next, we’ll discuss the consequences of not rebalancing, which may partly answer the above question.

Portfolio Drift

The consequence of not rebalancing is portfolio drift, meaning the weights of assets will increasingly skew towards a single asset, as shown below.

Initially, evenly distributed assets become imbalanced, leading to a lack of diversification and increased risk. The decrease in diversification is one reason for increased risk, but asset valuation increases also lead to higher risk. Higher valuations result in lower expected returns and higher risk. In the example above, Asset C gains the highest weight due to increased valuation, and the added risk of Asset C is not offset, so the overall portfolio risk rises.

The chart illustrates this point. The green line represents a continuously rebalanced portfolio with constant risk over time. The yellow line shows 20 simulated portfolios without rebalancing, with all their risks increasing over time. The red line indicates the median risk of all portfolios over time, far higher than the continuously rebalanced portfolio.

What can we infer from this? "Holding for the long-term" is a common saying, but long-term holding does not equate to rationality or wise decision-making. Instead, it’s not the best investment approach. We need to introduce rebalancing to offset the uncompensated high risk brought by portfolio drift.

What is the Right Frequency?

I hope I have convinced you that rebalancing is beneficial. The next question is, what should the rebalancing frequency be?

This question is crucial. People who do option delta hedging might understand that for options, continuous hedging would result in profits being transacted away by transactional costs. Hence, option traders don’t do continuous hedging; choosing the hedging frequency is a headache.

For rebalancing, we also consider transaction costs, but we are luckier than option traders because an optimal frequency exists for rebalancing.

Here, we revisit the value & momentum window issue. Previously, we mentioned that the momentum phenomenon exists in almost all assets, except the Japanese stock market. What is momentum? Winners keep rising, and losers keep falling. Thus, going long on good-performing assets and short on poor-performing assets yields long-term positive returns (exceeding the market risk premium).

Some might question, if long on winners and short on losers yields positive returns, shouldn’t we avoid rebalancing since it does the opposite: buying losers and selling winners? This is the typical Disposition Effect (selling winners too early and holding losers too long, damaging long-term wealth). This question is excellent, and the contradiction lies in the time point selection, which determines the rebalancing frequency.

Let’s look at the chart below,

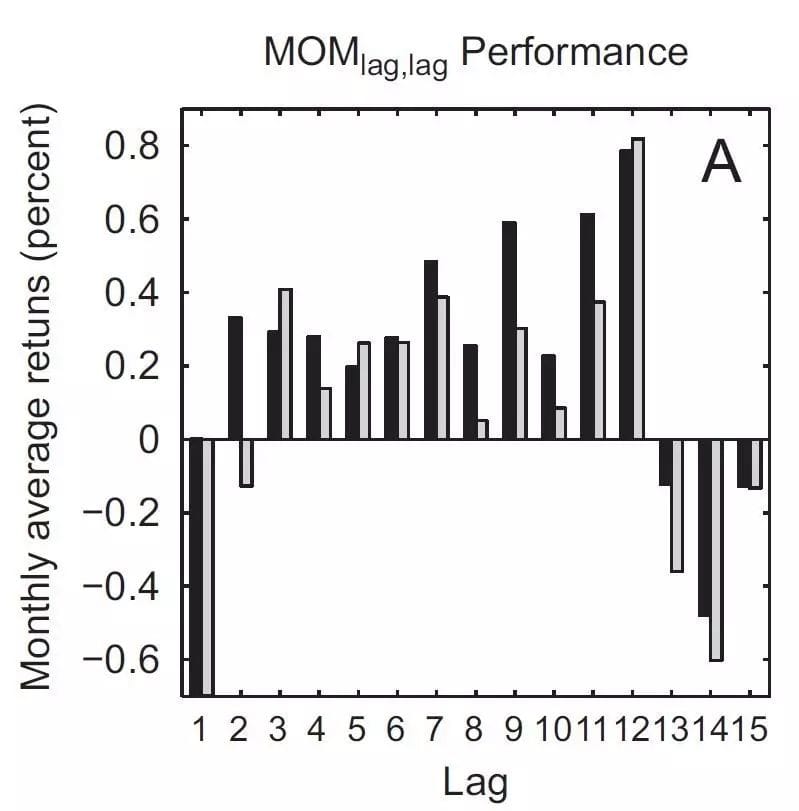
Market trends do not last forever; they are simply defined as positive autocorrelation for statisticians. The chart shows positive autocorrelation from one to twelve months, and negative autocorrelation beyond twelve months or within one month. In other words, going long (short) on assets that performed well (poorly) in the past 1-12 months generally yields positive returns, while going long (short) on assets beyond twelve months or within one month generally yields negative returns. This means reversals are more likely within one month and beyond twelve months. These reversals are significant enough to generate substantial returns through such price patterns. Annualised returns based on reversals within one month can be around 39%, considering transaction costs, explained more by behavioural finance.

What does this imply for rebalancing? Clearly, this price pattern suggests the best rebalancing frequency is over 12 months (though less than one month is theoretically feasible, it’s impractical as large-scale assets cannot be rapidly adjusted in the short term). High-frequency rebalancing essentially bets against trends. If trends outweigh the benefits of rebalancing, high-frequency rebalancing destroys value, unlike option delta hedging.

Consider the following portfolio example,

Let’s see the value created by rebalancing,

We can see that all rebalanced portfolios outperform Buy-and-Hold, with higher Sharpe Ratios. Annual rebalancing performs much better than monthly rebalancing, consistent with the above trend window discussion.

A Deep Look at Rebalancing

This section will discuss two different perspectives on rebalancing, both leading to similar conclusions.

Mathematically, rebalancing indeed yields long-term positive returns, a 100% positive return called Rebalancing Premium. Although called Premium, it involves no risk, hence my initial statement that rebalancing is a free lunch.

Claude Erb and Campell Harvey call it “turning water into wine,” while Igor Evstigneev and Claus Reiner Schenk-Hoppé term it “rags to riches.”

Rebalancing Premium derives from the well-known difference between Geometric and Arithmetic Returns, known as Jensen's Term.

When volatility is high, the difference between Geometric and Arithmetic Returns is the greatest. Long-term Rebalancing Premium depends on the underlying assets’ volatility, roughly 1/2*σ².

Because of this relationship between Rebalancing Premium and underlying asset volatility, high-volatility commodity markets exhibit extremely high Rebalancing Premiums, around 3.5%.

Before revealing another perspective on rebalancing, let’s do a rebalancing demo. Suppose you can only invest in stocks and bonds, with stocks having a 50% chance of doubling in price and a 50% chance of halving, as shown below.

Bonds give a 10% risk-free return. Initially, the stock/bond ratio is 60/40. Assume we hold for two years. Let’s first see the performance of a Buy-and-Hold strategy over two years,

Now consider rebalancing the portfolio to the original 60/40 ratio after one year,

Then compare Buy-and-Hold with Rebalancing,

What does this imply? The previous Binary Tree is the most primitive method of Option Pricing. If Buy-and-Hold is the X-axis, the rebalanced portfolio is equivalent to a short Straddle, as shown below.

Therefore, rebalancing compared to Buy-and-Hold equals shorting a Call Option and a Put Option. Verifying this with actual Option Selling shows complete alignment,

Thus, rebalancing is equivalent to shorting options/volatility (Volatility Selling). Unlike theoretical calculations, option pricing is based on implied volatility, not realised volatility. Volatility selling is a long-term profitable strategy (see below). Hence, Rebalancing Premium’s source is reducing risk (enhancing return’s central tendency, creating Jensen's Term) and Volatility Premium.

It’s surprising, but does it imply that rebalancing performs poorly during financial crises? I haven’t verified this, but academic consensus considers rebalancing a free lunch, perhaps primarily due to the first factor.

This article concludes here. I hope you recognise rebalancing’s power. The seemingly simple concept has much to explore. I will continue to follow new developments in rebalancing.

References

Hsu, J., 2015. The China Syndrome: Lessons from the A-Shares Bubble.

Eraker, B. and Ready, M., 2015. Do investors overpay for stocks with lottery-like payoffs? An examination of the returns of OTC stocks. Journal of Financial Economics, 115(3), pp.486-504.

Asness, C. and Liew, J., 2014. The great divide over market efficiency.Institutional Investor.

Faber, M.T. 2015. Global asset allocation: A survey of the world’s top asset allocation strategies. The Idea Farm .

Ilmanen, A. and Maloney, T., 2015. Portfolio Rebalancing (Part 1 of 2: Strategic Asset Allocation). AQR research.

Derman, E., 2004. My life as a quant: reflections on physics and finance. John Wiley & Sons.

Asness, C.S., Moskowitz, T.J. and Pedersen, L.H., 2013. Value and momentum everywhere. The Journal of Finance, 68(3), pp.929-985.

Frazzini, A., 2006. The disposition effect and underreaction to news. The Journal of Finance, 61(4), pp.2017-2046.

Novy-Marx, R., 2012. Is momentum really momentum?. Journal of Financial Economics, 103(3), pp.429-453.

Thaler, R., 2012. The winner's curse: Paradoxes and anomalies of economic life. Simon and Schuster.

Mitchell, M., Pedersen, L.H. and Pulvino, T., 2007. Slow moving capital (No. w12877). National Bureau of Economic Research.

Erb, C.B. and Harvey, C.R., 2006. The strategic and tactical value of commodity futures. Financial Analysts Journal, 62(2), pp.69-97.

Evstigneev, I.V. and Schenk-Hoppé, K.R., 2002. From rags to riches: on constant proportions investment strategies. International Journal of Theoretical and Applied Finance, 5(06), pp.563-573.

Disclaimer: The data and information mentioned are from third-party sources, and accuracy is not guaranteed. This article shares information and views, not professional investment advice. Consult professional advice before making investment decisions.

This article was originally written in Chinese and posted on my WeChat platform in 2016. The Chinese link can be found here